Machine Learning Prozess

Wie kann ich nun aber die Spielerleistung konkret berechnen? All meine Spielaktionen, die ich nun schon im SPADL-Format vorliegen habe, bekommen den Kontext der Spielsituation. Diese nennt man im Machine Learning Prozess Labels und Features.

Labels

Labels sind die Werte, die ich vorhersagen möchte. In meinem Fall sind das die Tore, die ein Spieler erzielt hat. Diese Werte sind die abhängige Variable, die ich mit meinen Features vorhersagen möchte. Um aus den bisherigen Daten zu lernen, welche Spielaktionen wahrscheinlich ein Tor ergeben, müssen die Tore in den Daten markiert werden. Die Tabelle mit meinen Spielaktionen bekommt nun zwei neue Spalten:

• scores: wird als True markiert, wenn in den nächsten 10 Aktionen ein Tor erzielt wird

• concedes: wird als True markiert, wenn in den nächsten 10 Aktionen ein Tor kassiert wird

Wieder wird darauf geachtet, ob die Spielaktion schon in einem früheren Durchgang bearbeitet wurde, um Rechenleistung zu sparen.

def compute_labels(spadl_h5: str, labels_h5: str) -> None:
    """
    Compute and store VAEP labels for each game in the given SPADL HDF5 file.

    Args:
        spadl_h5 (str): Path to the SPADL HDF5 file containing game actions.
        labels_h5 (str): Path to the HDF5 file where labels will be stored.

    Returns:
        None
    """
    games = pd.read_hdf(spadl_h5, "games")
    print("Number of games:", len(games))

    yfns = [lab.scores, lab.concedes, lab.goal_from_shot]

    labels = 0
    with pd.HDFStore(labels_h5) as store_labels:
        for game in tqdm.tqdm(list(games.itertuples()), desc=f"Computing and storing labels in {labels_h5}"):
            game_key = f"game_{game.game_id}"
            actions_key = f"actions/{game_key}"
            if game_key not in store_labels:
                labels += 1
                actions = pd.read_hdf(spadl_h5, actions_key)
                Y = pd.concat([fn(spadl.add_names(actions)) for fn in yfns], axis=1)
                store_labels.put(game_key, Y)

    print("Number of new labels:", labels)

Features

Features sind die Werte, die ich verwende, um die Labels vorherzusagen. In meinem Fall sind das die Spielaktionen, die ein Spieler durchgeführt hat. Diese Werte sind die unabhängigen Variablen, die ich verwende, um die abhängige Variable (die Tore) vorherzusagen.

Die Features, die ich verwenden möchte, ergeben sich aus den Informationen, die ich durch die Spielaktion erhalte. Mir stehen folgende Informationen zur Verfügung, aus denen ich Features ableiten kann:

• Zeit: In welcher Spielsekunde fand die Aktion statt?

• Ort: Wo fand die Aktion statt? Start- und Endpunkte jeder Aktion sind bekannt.

• Art der Aktion: War es ein Pass, ein Schuss, ein Dribbling oder ein Tackling?

• Resultat der Aktion: War die Aktion erfolgreich oder nicht?

• Körperteil: Mit welchem Körperteil wurde die Aktion ausgeführt?

Hieraus kann ich nun folgende Features ableiten:

• actiontype: Art der Aktion (Pass, Schuss, Dribbling, Tackling)

• bodypart: Körperteil, mit dem die Aktion ausgeführt wurde

• result: Ergebnis der Aktion (Success, Fail, OwnGoal, YellowCard, RedCard, Offside)

• goals_home: Anzahl der Tore des Heimteams nach der Aktion

• goals_away: Anzahl der Tore des Auswärtsteams nach der Aktion

• goals_diff: Differenz der Tore zwischen Heim- und Auswärtsteam nach der Aktion

• start_x: x-Koordinate des Startpunkts der Aktion

• start_y: y-Koordinate des Startpunkts der Aktion

• end_x: x-Koordinate des Endpunkts der Aktion

• end_y: y-Koordinate des Endpunkts der Aktion

• movement: Distanz, die der Spieler in der Aktion zurückgelegt hat

• space_delta: Distanz zwischen der letzten Aktion und der aktuellen Aktion

• start_polar: Polarkoordinaten des Startpunkts der Aktion als Tuple (Winkel, Distanz) zum gegnerischen Tor

• end_polar: Polarkoordinaten des Endpunkts der Aktion als Tuple (Winkel, Distanz) zum gegnerischen Tor

• team: Prüft, ob der Ballbesitz gewechselt hat zwischen den Aktionen

• time: Zeitpunkt der Aktion im Spiel

• time_delta: Zeitdifferenz zur letzten Aktion

Da Machine Learning-Algorithmen darauf ausgelegt sind, mit Zahlen bzw. Vektoren zu arbeiten, müssen die Features in numerische Werte umgewandelt werden. Das Verfahren, um kategorische Werte in numerische Werte umzuwandeln, wird oft als One-Hot-Encoding bezeichnet. Hierbei wird jede Kategorie in eine eigene Spalte umgewandelt und mit 0 oder 1 kodiert.

def compute_features(spadl_h5: str, features_h5: str) -> None:
    """
    Compute and store VAEP features for each game in the given SPADL HDF5 file.

    Args:
        spadl_h5 (str): Path to the SPADL HDF5 file containing game actions.
        features_h5 (str): Path to the HDF5 file where features will be stored.

    Returns:
        None
    """
    games = pd.read_hdf(spadl_h5, "games")
    print("Number of games:", len(games))

    xfns = [
        fs.actiontype,
        fs.actiontype_onehot,
        fs.bodypart,
        fs.bodypart_onehot,
        fs.result,
        fs.result_onehot,
        fs.goalscore,
        fs.startlocation,
        fs.endlocation,
        fs.movement,
        fs.space_delta,
        fs.startpolar,
        fs.endpolar,
        fs.team,
        fs.time,
        fs.time_delta
    ]

    features = 0
    with pd.HDFStore(features_h5) as store_features:
        for game in tqdm.tqdm(list(games.itertuples()), desc=f"Generating and storing features in {features_h5}"):
            game_key = f"game_{game.game_id}"
            actions_key = f"actions/{game_key}"
            if game_key not in store_features:
                features += 1
                actions = pd.read_hdf(spadl_h5, actions_key)
                gamestates = fs.gamestates(spadl.add_names(actions), 3)
                gamestates = fs.play_left_to_right(gamestates, game.home_team_id)

                X = pd.concat([fn(gamestates) for fn in xfns], axis=1)
                store_features.put(game_key, X)

    print("Number of new features:", features)

Das Machine Learning Modell

Hier zeige ich, wie ich ein ganz neues Modell trainiere. Im späteren Verlauf, wenn immer wieder neue Spiele hinzukommen, wird das bereits trainierte Modell genutzt, um damit die neuen Spiele zu bewerten, sodass nicht immer wieder ein neues Modell trainiert werden muss.

In Kurz: Ich brauche einen Algorithmus, der die kontextbezogenen Spielaktionen in zwei Klassen vorhersagt (Es wird ein Tor erzielt / Es wird kein Tor erzielt). Wichtig ist hierbei, dass ich aus der Vorhersagewahrscheinlichkeit für jede Spielaktion die Leistung eines Spielers ableiten kann.

Was passiert nun?

1. Ich lade alle Spiele und deren Labels und Features aus der HDF5-Datei.

2. Ich teile die Spiele in Trainings- und Testdaten auf. Die Trainingsdaten werden verwendet, um das Modell zu trainieren, während die Testdaten verwendet werden, um die Leistung des Modells zu bewerten. Eine Aufteilung im Bereich 70% Trainingsdaten und 30% Testdaten ist üblich, kann aber je nach Datensatz auch variieren.

games = pd.read_hdf(spadl_h5, "games")
    print("nb of games:", len(games))

    # Split games into training and test set
    train_test_ratio = 0.7
    games = games.sort_values(["game_date"]).reset_index(drop=True)
    train_size = int(len(games) * train_test_ratio)
    traingames = games[:train_size]
    testgames = games[train_size:]

3. Ich wähle die Features aus, die ich für das Training verwenden möchte und wähle die Anzahl der Spielaktionen aus, die ein Gamestate bilden. In meinem Fall sind das drei Aktionen. Hierbei ist zu beachten, dass die Anzahl der Features und die Anzahl der Aktionen in einem Gamestate die Rechenleistung erheblich beeinflusst.

    # Define the feature functions
xfns = [
    fs.actiontype, fs.actiontype_onehot, fs.bodypart, fs.bodypart_onehot, fs.result, fs.result_onehot,
    fs.goalscore, fs.startlocation, fs.endlocation, fs.movement, fs.space_delta, fs.startpolar, fs.endpolar,
    fs.team, fs.time, fs.time_delta
]
nb_prev_actions = 3
Xcols = fs.feature_column_names(xfns, nb_prev_actions)

4. Die Trainingsdaten laden und in das Modell übergeben. Als Modell wird hier ein XGBoost-Modell verwendet.

XGBoost

XGBoost ist eine leistungsstarke Bibliothek für maschinelles Lernen, die auf dem Gradient Boosting-Algorithmus basiert. Es ist besonders gut geeignet für strukturierte Daten und dabei als erfolgreich erwiesen. Der Algorithmus gehört zum supervised-learning (die Daten sind bereits gelabelt) und basiert auf Entscheidungsbäumen. Die Entscheidungsbäume werden nacheinander trainiert und verbessern sich dabei ständig, indem sie die Fehler der vorherigen Bäume korrigieren. Dieser Prozess wird als Boosting bezeichnet. Dieser Algorithmus gibt uns nicht nur eine Vorhersage, ob eine Aktion ein Tor zur Folge hat oder nicht, sondern auch noch die Wahrscheinlichkeit, mit der das passiert. Aus diesen Wahrscheinlichkeitsdifferenzen kann ich dann die Leistung eines Spielers ableiten.

Die eingegebenen Hyperparameter dienen als Startpunkt. In einem weiteren Kapitel werde ich näher auf die Optimierung dieser Parameter eingehen.

• n_estimators = 50: Dieser Parameter bestimmt die Anzahl der Bäume im Modell. Eine höhere Anzahl von Bäumen kann zu einer besseren Leistung führen, aber auch die Trainingszeit erhöhen und möglicherweise zu Überanpassung (Overfitting) führen. Es ist oft nützlich, diesen Wert zu optimieren, indem man verschiedene Werte testet.

• max_depth = 3: Dieser Parameter legt die maximale Tiefe der einzelnen Bäume fest. Eine geringere Tiefe verhindert Überanpassung, kann jedoch die Modellleistung einschränken, wenn das Modell nicht genügend Komplexität hat, um die Datenstruktur zu erfassen. Auch hier kann eine Optimierung durch Testen verschiedener Werte hilfreich sein.

• n_jobs = -1: Dieser Parameter gibt an, wie viele parallele Threads zur Verfügung stehen. Der Wert -1 bedeutet, dass alle verfügbaren Kerne genutzt werden, was die Trainingszeit auf Mehrkernprozessoren verkürzen kann. Dies ist in der Regel eine gute Wahl für schnellere Trainingszeiten.

• verbosity = 1: Dieser Parameter steuert die Menge der Ausgaben während des Trainings. Ein Wert von 1 gibt grundlegende Informationen aus. Für detailliertere Informationen kann ein höherer Wert verwendet werden, aber das ist eher eine Präferenzfrage und hat keinen Einfluss auf die Modellleistung.

Diese Parameter bieten eine solide Grundlage für das Trainieren der Modelle, können aber je nach Datensatz und Problemstellung angepasst werden, um die beste Leistung zu erzielen.

# Get training data
    X_train, Y_train = getXY(traingames, Xcols)
    print("X:", list(X_train.columns))
    print("Y:", list(Y_train.columns))

    # Train classifiers
    Y_hat = pd.DataFrame()
    models = {}
    for col in list(Y_train.columns):
        model = xgboost.XGBClassifier(n_estimators=50, max_depth=3, n_jobs=-1, verbosity=1)
        model.fit(X_train, Y_train[col])
        models[col] = model
        joblib.dump(model, f"{col}_model.pkl")

Beispiel Entscheidungsbaum

Hier noch einmal ein einfaches Beispiel, wie man sich so einen Entscheidungsbaum bezogen auf unser Thema vorstellen kann.

                                       actiontype
                                 /     |     |       \
                             Schuss  Pass Dribbling Tackling
                             /                          \
                       start_x > 75?                start_x > 75?
                         /       \                   /       \
                        Ja       Nein              Ja        Nein
                      /   \                      /   \
          bodypart = Fuß bodypart ≠ Fuß    space_delta > 10  space_delta ≤ 10
             /           \                   /        \        /        \
         start_y < 40   start_y ≥ 40     Tor     Kein Tor   Tor      Kein Tor
            / \           / \                   
          Tor Kein Tor  Tor Kein Tor

Modell Evaluierung

Hierfür wird das Modell mit den Testdaten geladen und die Vorhersagen mit den tatsächlichen Labels verglichen. Die Genauigkeit des Modells wird anhand verschiedener Metriken bewertet.

# Evaluate models
    testX, testY = getXY(testgames, Xcols)
    def evaluate(y: pd.Series, y_hat: pd.Series) -> None:
        p = sum(y) / len(y)
        base = [p] * len(y)
        brier = brier_score_loss(y, y_hat)
        print(f"  Brier score: {brier:.5f} ({brier / brier_score_loss(y, base):.5f})")
        ll = log_loss(y, y_hat)
        print(f"  log loss score: {ll:.5f} ({ll / log_loss(y, base):.5f})")
        print(f"  ROC AUC: {roc_auc_score(y, y_hat):.5f}")

    for col in testY.columns:
        Y_hat[col] = [p[1] for p in models[col].predict_proba(testX)]
        print(f"### Y: {col} ###")
        evaluate(testY[col], Y_hat[col])

Hier ein Beispiel für eine Modellbewertung, als ich zuletzt neue Spiele hinzugefügt habe:

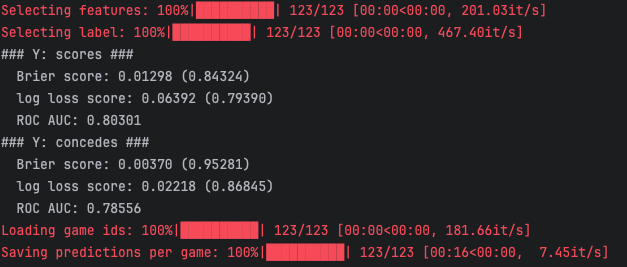
• Brier-Score: Der Brier-Score ist wie ein Fehlerpunkt. Er misst, wie nah meine Vorhersagen an den tatsächlichen Ergebnissen sind. Ein kleiner Brier-Score bedeutet, dass ich sehr gut geschätzt habe. Weitere Infos

• Log-Loss Score: Der Log-Loss-Score ist wie eine Strafe, die höher wird, je schlechter meine Vorhersagen sind. Je kleiner der Log-Loss-Score, desto besser meine Vorhersagen. Weitere Infos

• ROC-AUC Wert: Die ROC AUC-Werte zeigen eine gute Trennschärfe des Modells. Werte über 0.8 sind gut und deuten auf eine hohe Fähigkeit des Modells hin, zwischen den Klassen zu unterscheiden. Ein Wert von 1 bedeutet perfekt, und ein Wert von 0.5 bedeutet, dass es wie Raten ist.

Wahrscheinlichkeitswerte auslesen und VAEP-Werte berechnen

Das Ergebnis der Berechnungen sind nun die Wahrscheinlichkeitswerte für der Spielaktionen. Diese kann ich nun nutzen, um die VAEP-Werte für jede Aktion zu berechnen.

Zunächst einmal speichere ich die Predictions in der HDF5-Datei ab, um sie später wieder verwenden zu können. Anschließend berechne ich die VAEP-Werte für jede Aktion und speichere sie ebenfalls in der HDF5-Datei ab.

 # Save predictions per game
    A = []
    for game_id in tqdm.tqdm(games.game_id, "Loading game ids"):
        Ai = pd.read_hdf(spadl_h5, f"actions/game_{game_id}")
        A.append(Ai[["game_id"]])
    A = pd.concat(A).reset_index(drop=True)

    grouped_predictions = pd.concat([A, Y_hat], axis=1).groupby("game_id")
    for k, df in tqdm.tqdm(grouped_predictions, desc="Saving predictions per game"):
        df = df.reset_index(drop=True)
        df[Y_hat.columns].to_hdf(predictions_h5, f"game_{int(k)}")

Aus den Wahrscheinlichkeitswerten können wir nun die VAEP-Werte berechnen.

• Der offensive Wert einer Aktion wird berechnet als die Differenz der Wahrscheinlichkeiten ein Tor zu erzielen vor der Aktion und nach der Aktion.

• Der defensive Wert einer Aktion wird berechnet als die Differenz der Wahrscheinlichkeit ein Gegentor zu kassieren vor der Aktion und nach der Aktion.

• Die Summe aus offensivem und defensivem Wert ergibt den VAEP-Wert einer Aktion.

Hier werden alle Aktionen geladen und mit den Spielerdaten und Spieldaten verknüpft. Anschließend werden die VAEP-Werte berechnet und in einem DataFrame gespeichert.

A = []
    for game in tqdm.tqdm(list(games.itertuples()), desc="Loading actions"):
        actions = pd.read_hdf(spadl_h5, f"actions/game_{game.game_id}")
        actions = (
            spadl.add_names(actions)
            .merge(players, how="left")
            .merge(teams, how="left", )
            .sort_values(["game_id", "period_id", "action_id"])
            .reset_index(drop=True)
        )
        preds = pd.read_hdf(predictions_h5, f"game_{game.game_id}")
        values = vaepformula.value(actions, preds.scores, preds.concedes)
        A.append(pd.concat([actions, preds, values], axis=1))
    A = pd.concat(A).sort_values(["game_id", "period_id", "time_seconds"]).reset_index(drop=True)

Aus den aufsummierten Werten könnte ich nun schon eine Bewertung der Spielerleistung für einen beliebigen Zeitraum ableiten. Da Spiele mit mehr Spielminuten vermeintlich mehr Value generieren können, wird das VAEP-Rating an die Spielzeit angepasst und auf 90 Minuten normalisiert.

Für die Bundesliga 2023/24 sieht das Ergebnis für die Top 10 dann so aus (min. 1500 Spielminuten):

Spieler	Minuten	Verein	VAEP Rating	VAEP off.	VAEP def.	VAEP Value	VAEP Value off.	VAEP Value def.	Position
Harry Kane	3,084	Bayern	0.5787	0.5929	-0.0142	19.8317	20.3177	-0.486	FW
Robin Hack	1,533	Borussia M.Gladbach	0.4839	0.4988	-0.0149	8.2427	8.4968	-0.2541	FW
Jamal Musiala	1,882	Bayern	0.4366	0.4482	-0.0116	9.1294	9.372	-0.2426	AMC
Florian Wirtz	2,501	Leverkusen	0.4248	0.4365	-0.0117	11.8059	12.1298	-0.324	AMC
Donyell Malen	1,928	Borussia Dortmund	0.4234	0.4340	-0.0105	9.0711	9.2966	-0.2255	FWR
Kevin Stöger	2,820	Bochum	0.4129	0.4306	-0.0177	12.9383	13.4925	-0.5542	MC
Deniz Undav	2,234	Stuttgart	0.4123	0.4344	-0.0221	10.2338	10.7836	-0.5498	FW
Álex Grimaldo	2,929	Leverkusen	0.3971	0.4101	-0.0130	12.9242	13.3472	-0.423	DML
Benjamin Sesko	1,589	RBL	0.3883	0.4099	-0.0216	6.8553	7.2375	-0.3822	FW
Serhou Guirassy	2,347	Stuttgart	0.3793	0.4040	-0.0247	9.8924	10.5359	-0.6435	FW

Diese Daten möchte ich nun für weitere Berechnungen und Analysen speichern.